Guido's SSB Polar Modulation - Analysis and Application

This blog post is "work in progress" and may be updated from time to time. 

The uSDX, is a microprocessor-based Software Defined Transceiver developed by Guido PE1NNZ that has a very interesting technique to generate the SSB transmission. The SSB signal is created by rapidly updating both the output frequency and the output power of a class-E driven Power Amplifier. This design results in a power-efficient and very simple low cost circuit:

That's it - that's the entire transmit circuitry to generate a 5W SSB signal! That's crazy, and so much simpler than typical SSB modulation techniques. I'll call this type of modulation "polar modulation" for reasons that will become apparent later.

Guido's approach is such an attractive idea that the QMX is is also adopting polar modulation.  

This blog post describes my journey learning about polar modulation, how it works, what its limitations are, and how those limitations can be minimised in a practical implementation. The journey I took led me down many blind alleys. I'll try to spare you from these, and to chart a more direct and logical path.

My first step was to explore how it was even possible for polar modulation to modulate typical audio inputs. Understsanding it for a single input tone is easy - the output frequency and output power are just kept constant. For instance, if the transceiver is tuned to 7MHz upper sideband, and a modulating tone of 1kHz is applyed, the radio sets the si5351 CLK2 output frequency to 7.001MHz, and the PA amplitude to a value proportional to the input signal's amplitude. If the frequency or amplitude of the single tone modulating input changes, the output frequency and amplitude are updated accordingly.

When two audio signals, say at 1kHz and 1.9kHz, are applied then the output to the antenna should comprise two frequencies - one at 7.001MHz and one at 7.0019MHz. How is this possible when the transmitter is only capable of generating one frequency at a time? Well, it turns out that it is possible - by varying both the output frequency and output amplitude in exactly the right way. This can be shown mathematically in my blog post here.

I've gone on to confirm in both simulation software and laboratory-style tests that indeed a two frequency output signal can be accurately generated using polar modulation. However there are limitations to this approach which I will summarise here, and will explain later how I arrived at these conclusions.

Summary of Findings

The polar modulation algorithm is nonlinear, and becomes increasingly nonlinear as the amplitudes of two input tones approach each other.  When this happens, as with any nonlinear system, many harmonics are generated and these harmonics are at frequencies that are multiples of the difference-frequency of the input tones. For example, if the input signals are at 1kHz and 1.9kHz, the difference frequency is 900Hz, and there are harmonics at 1800Hz, 2700Hz, 3600Hz, etc.

The harmonics are critical to the correct generation of the RF output. By "magic" the harmonics generated by the frequency variations exactly cancel the harmonics generated by the amplitude variations, resulting in a clean RF signal. Any reduction in the harmonic signals that are caused by bandwidth limitations in either the frequency or amplitude paths will result in spurious signals in the output.

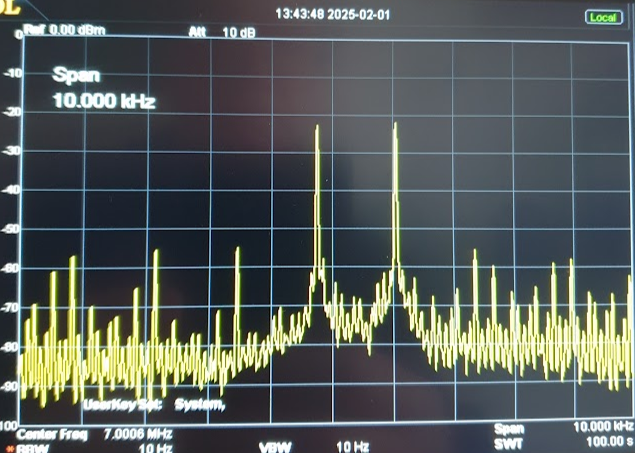
A rough rule of thumb for the case of equal-amplitude input signals is that the bandwidth of the frequency and amplitude paths need to be approximately 5x the maximum expected frequency-difference in order to keep the output's spurious signals more than 30dB below either test tone. For instance, the si5351 can only be updated at about 12ksps maximum (with overclocking the I2C bus beyond spec), and so has a maximum bandwidth of 6kHz. Such a system will show spurious signals of worse than 30dB whenever equal-amplitude dual-tone signals are applied that have a freequency difference greater than $\frac{6kHz}{5}=1200Hz$. However, as will be seen later, improvements are achievable if the amplitude path has a higher bandwidth than the frequency path.

To illustrate the consequences of limiting the bandwith of both paths, here is the simulation result of a 6kHz bandwidth limitation on 300Hz and 1600Hz tones (1300Hz frequency difference) is:

The same test on a laboratory hardware test set-up is:

Note the very strong similarity between the simulated results and real results (allowing for slightly difference horizontal and vertical scales). This is positive evidence of the accuracy of the simulation and my understanding of what is happening.

The Modulation Algorithm

The modulation algorithm at a high level is:

Or in pseudo-code:

modulate(audio): 

(I, Q) = HilbertTransform(audio)

amplitude = sqrt(I*I, Q*Q)

phase = atan2(Q, I)

deltaPhase = phase - lastPhase    // differentiate

lastPhase = phase

if (deltaPhase < 0)  deltaPhase = deltaPhase + 2*PI    // phase unwrapping

if (deltaPhase >PI) deltaPhase = deltaPhase - 2*PI     // phase unwrapping

frequency = deltaPhase * Const + CarrierFrequency

return (frequency, amplitude)

You might rightly wonder what is happening here - this is a huge jump from the description so far and from the mathematical analysis referred to above.

To understand how this algorithm works it helps to first describe:

1. The phasor representation of a sinusoid. 
2. The Hilbert transform, as it applies in this narrow application.
3. Phase unwrapping.

Phasor Representation

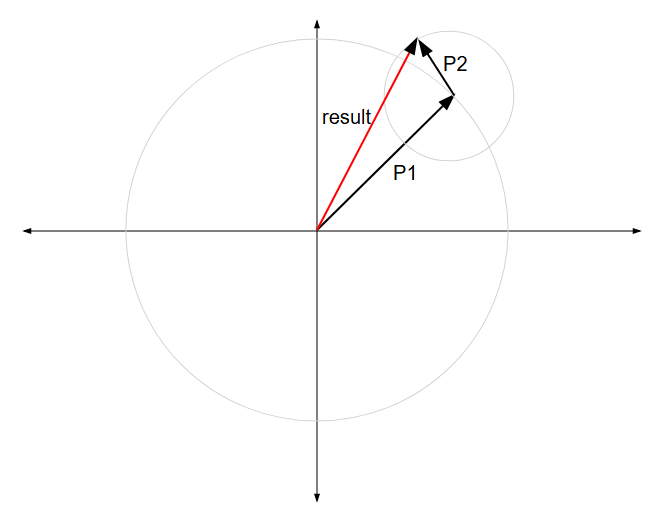
The key idea is that, since a sinusoid has both an amplitude and a phase, it can be represented as a vector(arrow) or phasor in a 2D space. The phasor's length is its amplitude, and its frequency is how quickly it rotates around its "tail" in this 2D space. So the tip of a phasor representing a single tone traces a circle in this 2D space. The convention is that the phasor rotates anticlockwise. The horizontal component of this phasor is the level of the signal we see. This is illustrated here.

At any point in time the phasor has a length (the distance from its tail to its tip) and an angle, which is the phasor's angle to the horizontal.

If a signal comprises multiple sinusoids, all the phasors representing these sinusoids are added together tip-to-tail, with each phasor continuing to rotate around its own tail. The result is a new result phasor with its tail at the origin and a tip that traces out a complex pattern in 2D space.

The resulting path could also be traced out by a hypothetical signal generator whose output amplitude and frequency is continually and precisely varied to match. The signal generator's output amplitude is the length of result phasor, and its frequency is the rate of change of the result phasor's angle. This is exactly the calculation being performed in the modulation algorithm!

The Hilbert Transform

The discussion above describes the use of phasors, but the input signal isn't in phasor form. That's where the Hilbert Transform (or Hilbert Filter) comes in - it turns the input into phasor form.

The Hilbert Transform takes an input sinusoid and through "magic" (which I don't understand) outputs two sinusoids I and Q, with Q delayed by exactly 90° compared to I. I and Q are the two dimensions of the 2D phasor space.

The Hilbert Transform is also linear, so if two sinusoids are combined and fed into the Hilbert Transform, the result is exactly the same as feeding each sinusoid into a separate Hilbert Transform and adding the result. ie 𝓗(a + b) = 𝓗(a) + 𝓗(b). This means we can feed our input signal, which comprises multiple frequencies, into the Hilbert Transform and the resulting I and Q signals correctly represent the result phasor described earlier.

Phase Unwrapping

We're almost there! The last issue to deal with is that the phase measurement only gives a raw value between -π and +π. But the actual phase angle of a sinusoid continues to grow without bound. This becomes an issue when we calculate the frequency by measuring the phase's rate of change.

If the raw atan2() phase value is used, the frequency calculation is incorrect each time the phase increases beyond π and jumps back to -π. That's why the following code is needed to "unwrap" the phase and to give the correct phase difference:

if (deltaPhase < 0)  deltaPhase = deltaPhase + 2*PI    // phase unwrapping

It is also possible for the phase be decreasing and for the phase to jump from -π to +π. The code to "unwrap" this case is:

if (deltaPhase >PI) deltaPhase = deltaPhase - 2*PI     // phase unwrapping

"When can the phase be decreasing - that's a negative frequency!" you might ask. Here's an example. Phasor 1 is rotating slowly (say at 100Hz), and Phasor 2 is rotating quickly (say at 1kHz). In the time that Phasor 2 rotates from position 1 to position 2 Phase 1 has hardly moved. The result phasor has moved from pointing to 1 to pointing at 2 - a reduction in phase:

This latter case of phase unwrapping is absent from the uSDX implementation, but appears to be unimportant since it makes little difference to the final signal. Update 29 Mar 2025: this latter case is important after all. Without it, there are increased spuri when the higher frequency tone has slightly lower amplitude than the lower frequency tone.

Studying the appropriate phasor diagrams helps illustrate why the mathematical analysis shows the phase changes so dramatically when the two frequencies are of similar amplitude:

In this diagram, the origin is towards the top, and a trace of the tip of the result phasor is shown over a number of time steps. The low frequency's phasor has its tail at the origin, and its tip is currently in the lower left quadrant. The higher frequency's phasor has it's tail at the LF phasor's tip, and since it is spinning much faster, it is causing the dominant movement; it's tip is the tip of the result phasor. It has similar amplitude to the LF phasor so the result phasor passes very close to, but slightly below, the origin.

For the majority of the result phasor's path, it's angle to the origin only changes relatively slowly from one time step to the next. However, the step from orange to purple, and from purple to red, are very dramatic negative phase changes. This is the dramatic phase change as predicted by the mathematical analysis.

Note that there's nothing special in this description about the LF phasor's location. Another "snapshot" could be taken at a different time where the LF phasor is pointing - say - in the upper right quadrant; exactly the same description of the phase behaviour would apply. In fact different snapshots in time can be thought of as just rotating this image around the origin.

If you now imagine that the HF phasor's amplitude is very slightly larger, then the result phasor would pass very close to, but slightly above, the origin. In this case the dramatic phase changes are positive. A small amplitude change has caused the sign of the phase "blip" to change.

As a final thought experiment, imagine the two amplitudes are exactly the same. In this case the result phasor passes directly through the origin. At one time step it will be on one side of the origin, and on the next time step is will be on the opposite side - a 180° or $\pi$ radians change. The frequency, which is the change in phase over time, will be $\frac{\pi }{dt}$, where dt = the time step duration. If the size of the time step is reduced, then the frequency at the point of crossing increases. This becomes important later - altering the size of the time step alters the result of the frequency calculation - because the calculation depends on a time-derivative.

 Conclusion

This post has hopefully given some intuition behind polar modulation. In a subsequent post I'll investigate the the bandwidth requirements via simulation and a hardware implementation.