Suppose we have an SSB Transmitter tuned to transmit at carrier frequency \(f_c\), upper sideband. With an input audio modulating signal of \(f_a\), the transmitter generates an output signal of \( f_c + f_a\). For example if the tuned frequency is 7.0MHz and the audio input is 1kHz, a signal at 7.001MHz is generated.
Similarly, two input audio modulating signals \(f_a\) with amplitude a, and \(f_b\) with amplitude b, the transmitter generates a signal comprising two frequencies, one at \( f_c + f_a\) and another at \( f_c + f_b\).
The following analysis shows that this 2-frequency output signal can be generated by amplitude-modulating an a single frequency-modulated oscillator.
The following trigonometric identities are used:
(I): \( \cos(x+y) = \cos x\cos y - \sin x\sin y\) -- link
(II) \(x\cos\theta + y\sin\theta = c\cos(\theta+\phi)\) where \( c = sgn(x)\sqrt{(x^2+y^2)}\), \(\phi = \arctan(-y/x)\) -- link
(III) \( \sin^2x + \cos^2x = 1\) -- link
We start with the output signal:
\( s = a\cos 2\pi(f_c+f_a)t + b\cos 2\pi(f_c+f_b)\)
Define \( \omega_c = 2\pi f_c \), \(\omega_a = 2\pi(f_c+f_a)\) and \(\omega_b = 2\pi(f_c+f_b)\):
\( s = a\cos \omega_a t + b\cos \omega_b \)
\( s = a\cos \omega_a t + b\cos (\omega_a t + (\omega_b - \omega_a) t)\)
Applying (I):
\( s = a\cos \omega_a t + b \cos \omega_a t \cos (\omega_b - \omega_a) t - b\sin\omega_a t \sin (\omega_b - \omega_a) t\)
Rearranging:
\( s = (a + b\cos (\omega_b - \omega_a) t) \cos\omega_a t - b\sin\omega_a t \sin (\omega_b - \omega_a) t\)
Applying (II), with \(x = (a + b\cos (\omega_b - \omega_a) t)\), \(y = b\sin(\omega_b - \omega_a)t\):
\(s = \sqrt{a^2 + 2ab\cos(\omega_b - \omega_a) t + b^2\cos^2(\omega_b - \omega_a) t + b^2\sin^2(\omega_b - \omega_a) t} \cos\left({\omega_a t +\tan^{-1} \frac{b\sin(\omega_b - \omega_a) t}{a+b\cos(\omega_b - \omega_a) t}}\right)\)
Applying (III) to simplify the terms under the square root:
\(s = \sqrt{a^2 + 2ab\cos(\omega_b - \omega_a) t + b^2} \cos\left({\omega_a t +\tan^{-1} \frac{b\sin(\omega_b - \omega_a) t}{a+b\cos(\omega_b - \omega_a) t}}\right)\)
This complex equation can be better understood by rewriting it as:
\(s = A \cos (\omega_a t + f(t))\)
where:
- \( A = \sqrt{a^2 + 2ab\cos(\omega_b - \omega_a) t + b^2} \) sets the amplitude of the generated signal, and varies slowly compared to the carrier frequency because \( \omega_b - \omega_a \ll \omega_c\), and
- \( f(t) = \tan^{-1} \frac{b\sin(\omega_b - \omega_a) t}{a+b\cos(\omega_b - \omega_a) t} \) and varies slowly compared to the \(\omega_a t\) term, again because \( \omega_b - \omega_a \ll \omega_c\).
In other words, combining two input signals results in an output signal with a phase varying around \(\omega_a t\) at the difference frequency \(\omega_b - \omega_a\) and with amplitude A also varying at the difference frequency.
Confidence that the formula is correctly derived can be gained by testing what happens if either of the modulating signals is removed (by setting it's amplitude term - either a or b - to zero. The formula should "collapse" to a single simple waveform. Indeed this is exactly what happens.
The analysis so far draws on "Frequency Analysis, Modulation and Noise", Standford Goldman, 1948 - p160. I believe what follows is novel.
Phase/Frequency Analysis
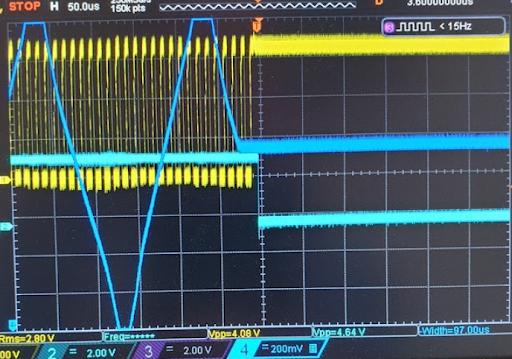
Experimenting with different values starts to give some slight intuition about how the amplitude values influence the frequency output. For instance, as the two amplitudes approach each other, the frquency variation grows dramatically:
Finally, when the two amplitudes are equal, there's a discontinuity & the "blip" disappears from the graph view - the negative "blip" is still there and corresponds to the negative edge of the input signal, but it's infinitely narrow and doesn't display:
The explanation for the discontinuities in the blue input waveform is that it is a phase measurement and has been displayed to wrap every \(2\pi\). The red derivative is displayed correctly and does not show any "blips" at these transitions.
Amplitude Analysis
The amplitude term is \( A = \sqrt{a^2 + 2ab\cos(\omega_b - \omega_a) t + b^2} \).
Its behaviour can be interactively plotted here.
The most interesting plot is again when \(a = b\):
This is a rectified sine wave, as can be demonstrated by setting \(a = b = 1\). The amplitude term simplifies to:
\( A = \sqrt{1 + 2\cos(\omega_b - \omega_a) t + 1} \)
\( A = \sqrt(2)\sqrt{1 + \cos(\omega_b - \omega_a) t } \)
But \(sgn(\cos\frac{\theta}{2})\sqrt{\frac{1 + \cos\theta}{2}}= \cos\frac{\theta}{2}\) (see link).
So, ignoring the sign term, the amplitude is the shape of a cosine wave.
A rectified sine wave has high harmonic content (see here or here), which will become relevant in later analysis.
Conclusions
This mathematical analysis has derived some equations for both amplitude and frequency shift that appear to correspond to expectations.
The interactive waveform plots give some intuition on the signal behaviour. In particular, when the two tones approach the same amplitude, the frequency shift approaches a discontinuity and values can become very large, and the amplitude waveform approaches a shape that has high harmonic content.